WEI-CHENG CHEN

說明

找出具有最大和的連續子數組

解題 01：前綴和

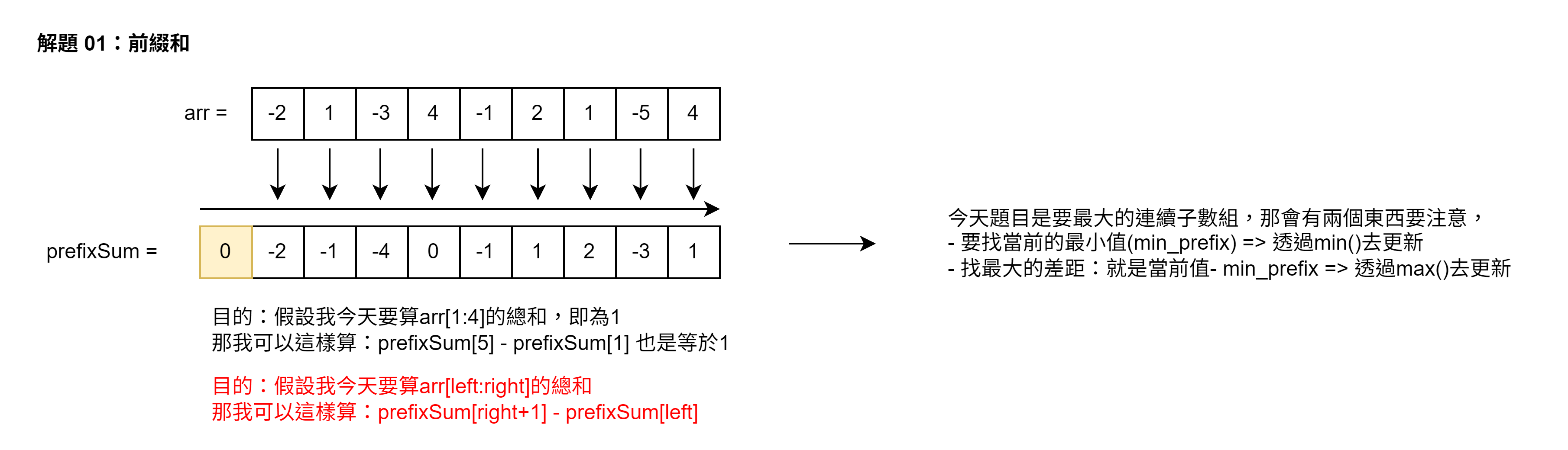
要先了解所謂的前綴和

e.g. arr = [-2, 1, -3, 4, -1, 2, 1, -5, 4]

這個陣列的前綴和即為 prefixSum = [0, -2, -1, -4, 0, -1, 1, 2, -3, 1] (一開始先塞一個 0)

建立好前綴和後，假如我要知道nums[left:tight]總和。即為prefixSum[right+1]-prefixSum[left]

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 前綴和陣列
        vector<int> prefixSum(nums.size() + 1, 0);
        for(int i=0;i<nums.size();i++){
            prefixSum[i + 1] = prefixSum[i] + nums[i];
        }

        // 接下來要找最大差值
        int ans = INT_MIN;
        int minPrefix = 0;
        for(int i=1;i<prefixSum.size();i++){
            ans = max(ans, prefixSum[i] - minPrefix);
            minPrefix = min(minPrefix, prefixSum[i]);
        }
        return ans;
    }
};

解題 02：DP

定義：dp[i] = 以nums[i]為結尾的最大連續數總和

• NOTE01：如果前一個的dp[i-1]小於 0，dp[i] = 0 + nums[i]
• NOTE02：如果前一個的dp[i-1]大於 0，dp[i] = dp[i-1] + nums[i]

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        // 前綴和陣列
        vector<int> dp(nums.size(), 0);
        dp[0] = nums[0];
        for(int i=1;i<nums.size();i++){
            if(dp[i-1]>0) dp[i] = dp[i-1] + nums[i]; // NOTE01
            else dp[i] = 0 + nums[i]; // NOTE02
        }

        return *max_element(dp.begin(), dp.end()); // 從陣列中找到最大值
    }
};